Question

Consider the set n of positive integers to be the universal set. sets​ h, t,​ e, and p are defined to the right. determine whether or not the sets upper e prime font size decreased by 10 and upper p prime are disjoint. h equals startset n is an element of upper n vertical line n greater than 100 endset t equals startset n is an element of upper n vertical line n less than 900 endset e equals startset n is an element of upper n vertical line n is even endset p equals startset n is an element of upper n vertical line n is prime endset

Answer 1

The sets E' and P' are not disjoint.

Explanation:

Definition: Two sets are disjoint if their intersection is an empty set.

The sets are defined as follows.

`\text{Universal Set}, U=\{n|n \in \mathbb{Z}^+\},$ where \mathbb{Z}^+$ is the set of positive integers.`

`H=\{n|n \in \mathbb{N}| n>100\}\\T=\{n|n \in \mathbb{N}| n<900\}\\E=\{n|n \in \mathbb{N}| n$ is even$\}\\P=\{n|n \in \mathbb{N}| n$ is prime\}`

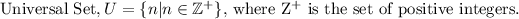
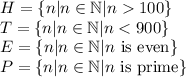
We are to determine if the sets E' and P' are disjoint.

E' and P' are the complements of E and P respectively.

Therefore:

`E'=\{n|n \in \mathbb{N}| n$ is odd$\}\\P'=\{n|n \in \mathbb{N}| n$ is not prime\}`

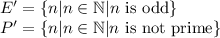
The intersection

`E' \cap P' =\{n|n \in \mathbb{N}| n$ is odd but not prime$\}`

Therefore, the sets E' and P' are not disjoint.