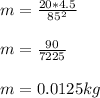Question

Transverse waves are sent along a 4.50 m long string with a speed of 85.00 m/s. The string is under a tension of 20.00 N. What is the mass of the string (in kg)?

Answer 1

m = 0.0125 kg

Step-by-step explanation:

Let us apply the formula for the speed of a wave on a string that is under tension:

`v = \sqrt{(F)/(\mu) }`

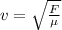
where F = tension force

μ = mass per unit length

Mass per unit length is given as:

μ = m / l

where m = mass of the string

l = length of the string

This implies that:

`v = \sqrt{(F)/(m/l) }\\ \\v = \sqrt{(F * l)/(m) }`

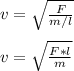
Let us make mass, m, the subject of the formula:

`v^2 = (F * l)/(m)\\\\m = (F * l)/(v^2)`

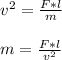
From the question:

F = 20 N

l = 4.50 m

v = 85 m/s

Therefore:

`m = (20 * 4.5)/(85^2)\\\\m = (90)/(7225)\\ \\m = 0.0125 kg`