Question

The magnitude of the magnetic flux through the surface of a circular plate is 6.80 10-5 T · m2 when it is placed in a region of uniform magnetic field that is oriented at 43.0° to the vertical. The radius of the plate is 8.50 cm. Determine the strength of the magnetic field. mT A circular plate of radius r is lying flat. A field of arrows labeled vector B rising up and to the right pass through the plate.

Answer 1

B = 4.1*10^-3 T = 4.1mT

Step-by-step explanation:

In order to calculate the strength of the magnetic field, you use the following formula for the magnetic flux trough a surface:

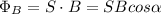`\Phi_B=S\cdot B=SBcos\alpha` (1)

ФB: magnetic flux trough the circular surface = 6.80*10^-5 T.m^2

S: surface area of the circular plate = π.r^2

r: radius of the circular plate = 8.50cm = 0.085m

B: magnitude of the magnetic field = ?

α: angle between the direction of the magnetic field and the normal to the surface area of the circular plate = 43.0°

You solve the equation (1) for B, and replace the values of the other parameters:

`B=(\Phi_B)/(Scos\alpha)=(6.80*10^(-5)T.m^2)/((\pi (0.085m)^2)cos(43.0\°))\\\\B=4.1*10^(-3)T=4.1mT`

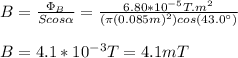
The strength of the magntetic field is 4.1mT