Question

An array of power transistors, dissipating 6 W of power each, are to be cooled by mounting them on a 25cm ×25cm-square aluminum plate and blowing air at 35°C over the platewith a fan at a velocity of 4 m/s. The average temperature of the plate is not to exceed 65°C. Assuming the heat transfer from the back side of the plate to be negligible and disregarding radiation, determine the number of transistors that can be placed on this plate

Answer 1

5

Step-by-step explanation:

Given:-

- The power dissipated by a transistor, q = 6 W

- The dimensions of the plate: ( 25 x 25 ) cm

- The forced velocity of air, V = 4 m/s

- The temperature of the air, T∞ = 35°C

- The temperature of the surface, Ts = 65°C

Declare Variables/Symbols:

- The number of transistors used = n

- Thermal conductivity = k

- Prandlt Number = Pr

- Nusselt Number ( averaged ) = Nu*

- Heat transfer coefficient ( averaged ) = h*

- Reynold's Number = Re

- Critical Reynold's Number ( Re,c ) = 5*10^5

- Density = ρ ( kg/m^3 )

- Dynamic Viscosity = μ ( kg/m.s )

Find:-

Assuming the heat transfer from the back side of the plate to be negligible and disregarding radiation, determine the number of transistors that can be placed on this plate

Solution:-

- We will perform the heat balance on the system ( aluminium plate integrated with transistors ). We will ignore the radiation effects and only consider the forced convective cooling of the transistors subjected to a stream of air forced at V = 4 m/s over the plate.

- From heat balance the rate at which heat is dissipated from the circuit -board is:

`n*q = h^*.A_s.( T_s - T_i_n_f )`

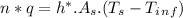
Where,

h*: The average heat transfer coefficient over the edge of the plate

As: The area exposed to convective current

- We need to determine the average heat transfer coefficient ( h* ) over the flat plate for the given conditions. We know that the heat transfer coefficient is a function of a dimensionless quantity ( Nu* ), thermal conductivity ( k ) of convection fluid and edge length of the plate ( L ).

- We will first determine the thermo-physical properties of the convective fluid ( air ). Its a standard practise to evaluate these properties at the film temperature ( T ) , i.e the average of surface temperature ( Ts ) and the free stream temperature ( T∞ ). Thus,

`T_f = (T_s + T_i_n_f)/(2) = (65 + 35)/(2)\\\\T_f = 50`

- Use thermo-physical tables ( A - 4 ) and evaluate properties at T = 50°C:

k = 0.02735 W /m.K

Pr = 0.7228

ρ = 1.092 kg/m^3

μ = 1.963*10^-5 kg/m.s

- The average Nusselt Number ( Nu* ) is a function of flow properties of the convective fluid namely: ( Re , Pr ). We will determine the Reynold's number over the edge of the aluminium plate as follows:

`Re_L = (p*V*L)/(u) = (1.092*4*0.25)/(1.963*10^-^5) = 55629.1391`

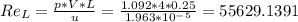
- The Reynold's number define the flow conditions of the fluid. We see that Reynold number calculated above is within the critical Reynold's number ( Re,c ). Therefore,

Re = 5.6 * 10^5 ≤ Re,c ( 5*10^5 )

- For flows with Re < Re,c, we take the assumption of "Laminar Boundary Layer".

- The corresponding (averaged) Nusselt Number empirical relation for Laminar flow regime and constant surface temperature ( Ts = 65°C ) over flat plate ( forced convection) we have:

`Nu^* = 0.664. Re_L^(1)/(2). Pr^(1)/(3)\\\\Nu^* = 0.664. (55629.13907)^(1)/(2). (0.7228)^(1)/(3)\\\\Nu^* = 140.5482`

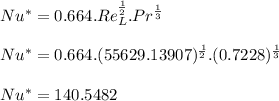
- From above relation we can evaluate the average heat transfer coefficient ( h* ) as follows:

`h^* = (Nu_L^*. k)/(L) = (140.5482. 0.02735)/(0.25)\\\\h^* = 15.376 (W)/(m^2.K)`

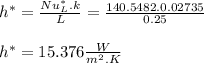
- Now we can use the energy balance applied to the system initially developed and solve for ( n ):

`n = (h^*. A_s. ( Ts - T_i_n_f))/(q) \\\\n = (15.376. ( 0.25)^2 . ( 65 - 35))/(6) \\\\n = 4.8`

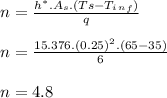
Answer: The number of transistors that can be placed are 5.

Note: In the above evaluation we have made an assumption that the exposed area ( As ) is equivalent to the surface area of the aluminium plate. This neglects the area associated with the thickness of the transistors. Moreover, we have assumed that the back-side of plate is thermally insulated. Also the surface temperature ( Ts ) of the plate base and the top of the transistor is assumed to be similar (if not then, we would have applied extended fin analysis ).