Question

Water pours into a tank at the rate of 2000 cm3/min. The tank is cylindrical with radius 2 meters. How fast is the height of water in the tank changing when the height of the water is 50 cm?

Answer 1

Volume of water in the tank:

`V=\pi (2\,\mathrm m)^2h=\pi(200\,\mathrm{cm})^2h`

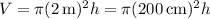
Differentiate both sides with respect to time t :

`(\mathrm dV)/(\mathrm dt)=\pi(200\,\mathrm{cm})^2(\mathrm dh)/(\mathrm dt)`

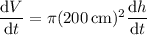
V changes at a rate of 2000 cc/min (cubic cm per minute); use this to solve for dh/dt :

`2000\frac{\mathrm{cm}^3}{\rm min}=\pi(40,000\,\mathrm{cm}^2)(\mathrm dh)/(\mathrm dt)`

`(\mathrm dh)/(\mathrm dt)=(2000)/(40,000\pi)(\rm cm)/(\rm min)=\frac1{20\pi}(\rm cm)/(\rm min)`

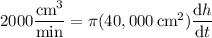
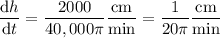
(The question asks how the height changes at the exact moment the height is 50 cm, but this info is a red herring because the rate of change is constant.)