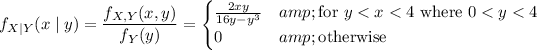Question

Given a joint PDF, f subscript X Y end subscript (x comma y )equals c x y comma space 0 less than y less than x less than 4, (1) (5 pts) Determine the constant c value such that the above joint PDF is valid. (2) (6 pts) Find P (X greater than 2 comma space Y less than 1 )(3) (9 pts) Determine the marginal PDF of X given Y

Answer 1

(1) Looks like the joint density is

`f_(X,Y)(x,y)=\begin{cases}cxy&\text{for }0<y<x<4\\0&\text{otherwise}\end{cases}`

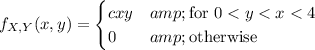
In order for this to be a proper density function, integrating it over its support should evaluate to 1. The support is a triangle with vertices at (0, 0), (4, 0), and (4, 4) (see attached shaded region), so the integral is

`\displaystyle\int_0^4\int_y^4 cxy\,\mathrm dx\,\mathrm dy=\int_0^4\frac{cy}2(4^2-y^2)=32c=1`

`\implies\boxed{c=\frac1{32}}`

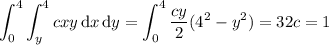
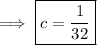
(2) The region in which X > 2 and Y < 1 corresponds to a 2x1 rectangle (see second attached shaded region), so the desired probability is

`P(X>2,Y<1)=\displaystyle\int_2^4\int_0^1(xy)/(32)\,\mathrm dy\,\mathrm dx=\boxed{\frac3{32}}`

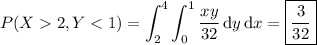
(3) Are you supposed to find the marginal density of X, or the conditional density of X given Y?

In the first case, you simply integrate the joint density with respect to y:

`f_X(x)=\displaystyle\int_(-\infty)^\infty f_(X,Y)(x,y)\,\mathrm dy=\int_0^x(xy)/(32)\,\mathrm dy=\begin{cases}(x^3)/(64)&\text{for }0<x<4\\0&\text{otherwise}\end{cases}`

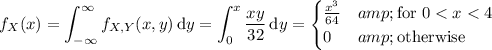
In the second case, we instead first find the marginal density of Y:

`f_Y(y)=\displaystyle\int_y^4(xy)/(32)\,\mathrm dx=\begin{cases}(16y-y^3)/(64)&\text{for }0<y<4\\0&\text{otherwise}\end{cases}`

Then use the marginal density to compute the conditional density of X given Y:

`f_(X\mid Y)(x\mid y)=(f_(X,Y)(x,y))/(f_Y(y))=\begin{cases}(2xy)/(16y-y^3)&\text{for }y<x<4\text{ where }0<y<4\\0&\text{otherwise}\end{cases}`