Question

Calculus Help!

So, I did this power series problem and found my summation notation, but when I found my limit it was
`(n)/(n+1)` after doing the Ratio Test and this would give ∞/∞. So with that in mind...

If the limit you got from your power series when doing a Ratio test was ∞/∞, would I have to do L'Hopital's Rule to get a number in order to define the interval of convergence? Or would that ∞/∞ tell you that it is divergent?

Answer 1

Yes.

Explanation:

You would have to use L'Hopital's Rule. Infinity/Infinity is undefined, just like 0/0 is undefined.

I just googled this.

Before trying other techniques, plug in the arrow number. If the result is:

A number, you’re done.

A number over zero or infinity over zero, the answer is infinity.

A number over infinity, the answer is zero.

0/0 or ∞/∞, use L’Hôpital’s Rule.

The thing is, when you say you got your limit, do you mean
`\lim_(n \to \infty) (n+1)/n` ?

This can just be found out by dividing by highest denominator power on numerator and denominator..

`\lim_(n \to \infty) 1 + 1/n`

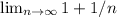
the limit of 1 is 1.

the limit of 1/x is 0.

because its equal to one it diverges.