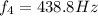Answer:
i
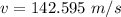
ii
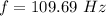
iii1 )
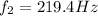
iii2)

iii3)
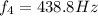
Step-by-step explanation:
From the question we are told that
The length of the string is
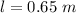
The tension on the string is
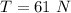
The mass per unit length is
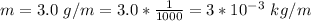
The speed of wave on the string is mathematically represented as

substituting values
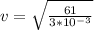
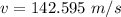
generally the string's frequency is mathematically represented as
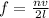
n = 1 given that the frequency we are to find is the fundamental frequency
So
substituting values
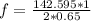
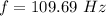
The frequencies at which the string would vibrate include
1

Here
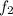 is know as the second harmonic and the value is
is know as the second harmonic and the value is

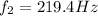
2
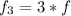
Here
 is know as the third harmonic and the value is
is know as the third harmonic and the value is


3
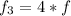
Here
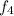 is know as the fourth harmonic and the value is
is know as the fourth harmonic and the value is