The question is incomplete! Complete question along with answer and step by step explanation is provided below.
Question:
Workers at a certain soda drink factory collected data on the volumes (in ounces) of a simple random sample of 18 cans of the soda drink. Those volumes have a mean of 12.19 oz and a standard deviation of 0.14 oz, and they appear to be from a normally distributed population.
If the workers want the filling process to work so that almost all cans have volumes between 12.02 oz and 12.66 oz, the range rule of thumb can be used to estimate that the standard deviation should be less than 0.16 oz. Use the sample data to test the claim that the population of volumes has a standard deviation less than 0.16 oz. Use a 0.01 significance level. Complete parts (a) through (d) below.
a. Identify the null and alternative hypotheses.
b. Compute the test statistic.
c. Find the p-value.
d. State the conclusion.
Answer:
Null hypotheses = H₀: σ = 0.16 oz
Alternate hypotheses = H₁: σ < 0.16 oz
Critical value = 6.408
Chi-square value =
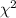 = 13.016
= 13.016
Reject H₀ Since
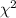 > Critical value
> Critical value
Reject H₀ Since p-value ≤ α
We have significant evidence at given significance level that the population of volumes has a standard deviation of less than 0.16 oz.
Explanation:
Set up hypotheses:
The null hypotheses is that the population of volumes has a standard deviation of 0.16 oz
Null hypotheses = H₀: σ = 0.16 oz
The claim to be tested is that the population of volumes has a standard deviation of less than 0.16 oz
Alternate hypotheses = H₁: σ < 0.16 oz
Determine type of test:
Since the alternate hypothesis states that the population of volumes has a standard deviation of less than 0.16 oz, therefore we will use a lower-tailed chi-square test.
Determine the Critical value:
Given level of significance = 0.01
Since it is a lower-tailed test, the areas given in the chi-square table are the areas to the right of the critical value. To get the areas on the left, subtract it from one, and then look it up
α = 1 - 0.01 = 0.99
degree of freedom = df = n - 1 = 18 - 1 = 17
The critical value from the chi-square table at α = 0.99 and df = 17 is found to be
Critical value = 6.408
Using an online “chi-square p-value calculator”
The left tail p-value for df = 17 and Critical value = 6.408 is found to be
p-value = 0.01
Set up decision rule:
Reject H₀ If > Critical value
We reject the Null hypothesis If the calculated chi-square value is more than the critical value.
OR
Reject H₀ If p-value ≤ α
Compute the test statistic:
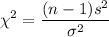
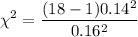
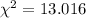
Conclusion:
We reject H₀
Since
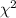 > Critical value
> Critical value
13.016 > 6.408
Also
p-value ≤ α
0.01 ≤ 0.01
We have significant evidence at given significance level that the population of volumes has a standard deviation of less than 0.16 oz.