Question

What is the equation of the line described below written in slope-intercept form? The line passing through point (0,0) and parallel to the line whose equation is 3x+2y-6=0

Answer 1

`y = - ( 3)/(2) x`

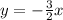
Explanation:

slope-intercept form

y= mx +c, where m is the slope and c is the y-intercept.

Let's rewrite the given equation into the slope-intercept form so we can find out its gradient.

3x +2y -6= 0

2y= -3x +6

Dividing by 2 throughout:

`y = - (3)/(2) x + 3`

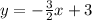
Thus gradient of given line=
`- (3)/(2)`

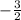
Parallel lines have the same gradient.

Thus gradient of line=
`- (3)/(2)`

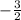
Subst. m=
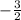`- (3)/(2)` into the equation:

`y = - (3)/(2)x + c`

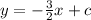
To find c, substitute a pair of coordinates.

When x=0, y=0,

`0 = - (3)/(2) (0) + c \\ c = 0`

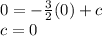
Thus, the equation of the line is
`y = - (3)/(2) x`.