Answer:
The 99% confidence interval estimate of the percentage of girls born is between 85.46% and 94.54%.
Usually, babies are equally as likely to be boys or girls. Here, it is desired to increase the probability of conceiving a girl, which is achieved, considering the lower bound of the confidence interval is considerably above 50%.
Explanation:
Confidence interval for the proportion:
In a sample with a number n of people surveyed with a probability of a success of
 , and a confidence level of
, and a confidence level of
 , we have the following confidence interval of proportions.
, we have the following confidence interval of proportions.

In which
z is the zscore that has a pvalue of
 .
.
For this problem, we have that:
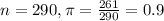
99% confidence level
So
 , z is the value of Z that has a pvalue of
, z is the value of Z that has a pvalue of
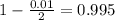 , so
, so
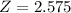 .
.
The lower limit of this interval is:
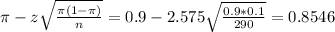
The upper limit of this interval is:
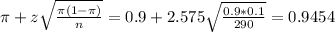
Percentage:
Proportion multplied by 100.
0.8546*100 = 85.46%
0.9454*100 = 94.54%
The 99% confidence interval estimate of the percentage of girls born is between 85.46% and 94.54%.
Based on the result, does the method appear to be effective?
Usually, babies are equally as likely to be boys or girls. Here, it is desired to increase the probability of conceiving a girl, which is achieved, considering the lower bound of the confidence interval is considerably above 50%.