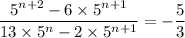Answer:
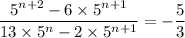
Explanation:
We are given the expression to be simplified:
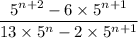
Let us take common a term with a power of 5 from the numerator and the denominator of the given expression.
We know that:
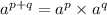
Let us use it to solve the powers of 5 in the given expression.
 we can write:
we can write:

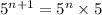
The given expression becomes:
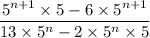
Taking common
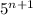 from the numerator and
from the numerator and
Taking common
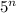 from the denominator
from the denominator
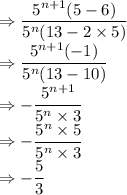
 The answer is:
The answer is: