Answer:
B
Explanation:
A rational expression is undefined when the denominator of the expression equals 0 (this is because anything over 0 is undefined). In other words, to find the values for which the given expression is undefined, we simply have to find the zeros of the denominator. We can ignore the numerator. Thus, let:
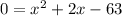
This is now a quadratic. Solve for the quadratic. I will factor but you can do whatever you like (complete the square, quadratic formula, etc.).
We notice that two factors that multiply to -63 and also add to +2 is 9 and -7. Thus:
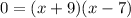
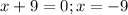
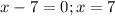
The zeros are -9 and 7.
The denominator will equal 0 at these values, and the expression will be undefined.