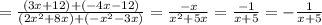Question

Please also provide details steps to this answer. PLEASE HELP ME!

Answer 1

`\left(\frac3{x+3}-\frac4{x+4}\right)/\left((2x)/(x+3)-\frac x{x+4}\right)=\\\\\\=\left((3(x+4))/((x+3)(x+4))-(4(x+3))/((x+4)(x+3))\right)/\left((2x(x+4))/((x+3)(x+4))-(x(x+3))/((x+4)(x+3))\right)=\\\\\\=(3(x+4)-4(x+3))/((x+3)(x+4))/(2x(x+4)-x(x+3))/((x+3)(x+4))=\\\\\\=(3x+12-4x-12)/((x+3)(x+4))*((x+3)(x+4))/(x[2(x+4)-(x+3)])=\\\\\\=(-x)/((x+3)(x+4))*((x+3)(x+4))/(x(2x+8-x-3))=\\\\\\=\frac{-1}1*\frac1{x+5}\ =\ -\frac1{x+5}`

Answer 2

C

Explanation:

First, to make things simpler, let's create a common denominator for every term. We can do this by multiplying (x+4) and (x+3) when the denominator has a (x+3) or (x+4), respectively. In other words:

`((3)/(x+3) -(4)/(x+4))/ ((2x)/(x+3)-(x)/(x+4))`

`((3(x+4))/((x+3)(x+4))-(4(x+3))/((x+4)(x+3))) / ((2x(x+4))/((x+3)(x+4)) -(x(x+3))/((x+4)(x+3)) )`

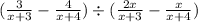
Now that they all have a common denominator, we can combine them:

`((3(x+4)-4(x+3))/((x+3)(x+4)))/ ((2x(x+4)-x(x+3))/((x+3)(x+4)) )`

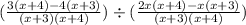
Now, divide them. Recall how to divide fractions. You "flip" the second term and change the division sign into a multiplication sign.

`=((3(x+4)-4(x+3))/((x+3)(x+4)))\cdot (((x+3)(x+4))/(2x(x+4)-x(x+3)) )`

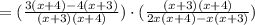
Notice the denominator of the first term and the numerator of the second; we can cancel them out.

`=(3(x+4)-4(x+3))/(2x(x+4)-x(x+3))`

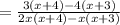
Now, we just need to simplify.

`=((3x+12)+(-4x-12))/((2x^2+8x)+(-x^2-3x)) =(-x)/(x^2+5x) =(-1)/(x+5)=-(1)/(x+5)`