Answer:
For the function
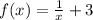 . The domain is
. The domain is
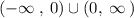 and the range is
and the range is
 .
.
For the function
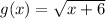 . The domain is
. The domain is
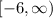 and the range is
and the range is
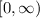 .
.
Explanation:
The domain of a function is the set of input or argument values for which the function is real and defined.
The range of a function is the complete set of all possible resulting values of the dependent variable, after we have substituted the domain.
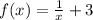 is a rational function. A rational function is a function that is expressed as the quotient of two polynomials.
is a rational function. A rational function is a function that is expressed as the quotient of two polynomials.
Rational functions are defined for all real numbers except those which result in a denominator that is equal to zero (i.e., division by zero).
The domain of the function is
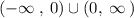 .
.
The range of the function is
 .
.
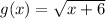 is a square root function.
is a square root function.
Square root functions are defined for all real numbers except those which result in a negative expression below the square root.
The expression below the square root in
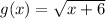 is
is
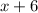 . We want that to be greater than or equal to zero.
. We want that to be greater than or equal to zero.
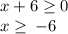
The domain of the function is
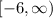 .
.
The range of the function is
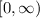 .
.