Question

A researcher wants to study the average miles run per day for marathon runners. In testing the hypotheses: H0: μ = 25 miles vs. H1: μ ≠ 25 miles, a random sample of 36 marathon runners drawn from a normal population whose standard deviation is 10, produced a mean of 22.8 miles weekly. What is the rejection region associated with 3% significance level?

Answer 1

The calculated value |Z| = 1.325 < 1.881 at 0.03 level of significance

Null hypothesis is accepted

Alternative hypothesis is rejected

A researcher wants to study the average miles run per day for marathon runners is 25

Explanation:

Step(i):-

Given sample size 'n' = 36

Given mean of the sample x⁻ = 22.8 miles

Given mean of the Population 'μ' = 25

Given standard deviation of the Population 'σ' = 10

Null hypothesis:-H₀: μ = 25

Alternative Hypothesis:H₁:μ ≠ 25

Level of significance = 3 % or 97%

The critical value Z₀.₉₇ = 1.881

Step(ii):-

Test statistic

`Z = (x^(-) - mean)/((S.D)/(√(n) ) )`

`Z = (22.8 - 25)/((10)/(√(36) ) )`

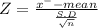
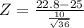
Z = -1.325

|Z| = |-1.325| = 1.325

The calculated value |Z| = 1.325 < 1.881 at 0.03 level of significance

Null hypothesis is accepted

Alternative hypothesis is rejected

conclusion:-

A researcher wants to study the average miles run per day for marathon runners is 25