Answer:
a) P(1) = 0.1637
b)

c) E(x) = 0.2
Explanation:
If X follows a poisson distribution, the probability that a disk has exactly x missing pulses is:
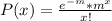
Where m is the mean and it is equal to the value of lambda. So, replacing the value of m by 0.2, we get that the probability that a disk has exactly one missing pulse is equal to:
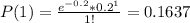
Additionally, the probability that a disk has at least two missing pulses can be calculated as:

Where
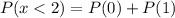 .
.
Then,
 and
and
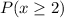 are calculated as:
are calculated as:
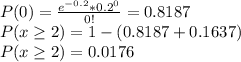
Finally, In the poisson distribution, E(x) is equal to lambda. So E(x) = 0.2