Question

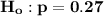
A genetic experiment involving peas yielded one sample of offspring consisting of 437437 green peas and 129129 yellow peas. Use a 0.050.05 significance level to test the claim that under the same​ circumstances, 2727​% of offspring peas will be yellow. Identify the null​ hypothesis, alternative​ hypothesis, test​ statistic, P-value, conclusion about the null​ hypothesis, and final conclusion that addresses the original claim. Use the​ P-value method and the normal distribution as an approximation to the binomial distribution.

Answer 1

The null hypothesis:
`\mathbf{H_o: p=0.27}`

The alternative hypothesis:
`\mathbf{H_1: p \\eq 0.27}`

Test statistics : z = −2.30

P-value: = 0.02144

Decision Rule: Since the p-value is lesser than the level of significance; then we reject the null hypothesis.

Conclusion: We accept the alternative hypothesis and conclude that under the same​ circumstances the proportion of offspring peas will be yellow is not equal to 0.27

Explanation:

From the given information:

Let's state the null and the alternative hypothesis;

Since The claim is that 27% of the offspring peas will be yellow.

The null hypothesis state that the proportion of offspring peas will be yellow is equal to 0.27.

i.e

`\mathbf{H_o: p=0.27}`

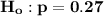
The alternative hypothesis state that the proportion of offspring peas will be yellow is not equal to 0.27

`\mathbf{H_1: p \\eq 0.27}`

The test statistics:

we are given 437 green peas and 129 yellow apples;

Hence;

`\hat p = (x)/(n)`

where ;

`\hat p` = sample proportion

x = number of success

n = total number of the sample size

`\hat p = (129)/(437+129)`

`\hat p = (129)/(566)`

`\mathbf{\hat p = 0.2279}`

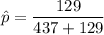
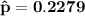
Now; the test statistics can be computed as :

`z = \frac { \hat p -p }{\sqrt {(p(1-p))/(n) } }`

`z = \frac {0.2279 -0.27 }{\sqrt {(0.27(1-0.27))/(566) } }`

`z = \frac {-0.043 }{\sqrt {(0.27(0.73))/(566) } }`

`z = \frac {-0.043 }{\sqrt {(0.1971)/(566) } }`

`z = \frac {-0.043 }{\sqrt {3.48233216*10^(-4) } }`

`z = \frac {-0.043 }{0.01866} }`

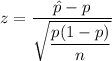
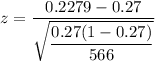
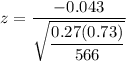
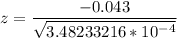
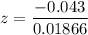
z = −2.30

C. P-value

P-value = P(Z < z)

P-value = P(Z< -2.30)

By using the ​ P-value method and the normal distribution as an approximation to the binomial distribution.

from the table of standard normal distribution

move left until the first column is reached. Note the value as –2.0

move upward until the top row is reached. Note the value as 0.30

find the probability value as 0.010724 by the intersection of the row and column values gives the area to the left of

z = -2.30

P- value = 2P(z ≤ -2.30)

P-value = 2 × 0.01072

P - value = 0.02144

Decision Rule: Since the p-value is lesser than the level of significance; then we reject the null hypothesis.

Conclusion: We accept the alternative hypothesis and conclude that under the same​ circumstances the proportion of offspring peas will be yellow is not equal to 0.27