Question

Which of the following changes will increase the frequency of the lowest frequency standing sound wave on a stretching string?Choose all that apply.A. Replacing the string with a thicker stringB. Plucking the string harderC. Doubling the length of the string

Answer 1

A, C

Step-by-step explanation:

Since the frequency is inversely proportional to the length of a string, then I want to increase the frequency of the lowest

A. Replacing the string with a thicker string.

Thicker strings have more density. The more density the string has, the lower the sound.

Mathematically, we can see the proportionality (direct and inverse) by looking at those formulas for Frequency and Speed, when combined:

For:

`f=(v)/(\lambda)`

`f=(v)/(\lambda)*\sqrt{(T)/(D) }`

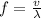
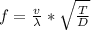
See above, how density (D) and
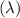`(\lambda)` wave length are inversely proportional.

C. Doubling the length of the string.

Because the length of the string is inversely proportional to the frequency.

The longer the string, the lower the frequency.

So, if we double string, we'll hear lower sounds in any string instrument

--

In short, for A, and C We can justify both since length and density are inversely proportional to the Frequency, we need longer or thicker string.