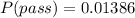Question

Pat Statsdud is taking an economics course. Pat's exam strategy is to rely on luck for the next exam. The exam consists of 20 multiple-choice questions. Each question has four possible answers, only one of which is correct. Pat plans to guess the answer to each question without reading it. If a grade on the exam is 50% or more, Pat will pass the exam. Find the probability that Pat will pass the exam.

Answer 1

0.01386 or 1.386%

Explanation:

Each question has a binomial distribution with probability of success p =0.25 (1 correct answer out of four alternatives).

The probability of 'k' successes in n trials is given by:

`P(x=k)=(n!)/((n-k)!k!)*p^k*(1-p)^(n-k)`

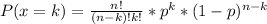
Pat will pass the exam if x ≥ 10. The probability that Pat will pass is:

`P(pass)=P(x=10)+P(x=11)+P(x=12)+P(x=13)+P(x=14)+P(x=15)+P(x=16)+P(x=17)+P(x=18)+P(x=19)+P(x=20)`

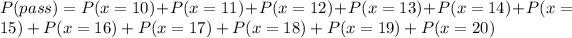
The probability for each number of success is:

`P(x=10)=(20!)/((20-10)!10!)*0.25^(10)*0.75^(10)=0.0099\\\\P(x=11)= (20!)/((20-11)!11!)*0.25^(11)*0.75^(9)=0.0030\\\\P(x=12)=(20!)/((20-12)!12!)*0.25^(12)*0.75^(8)=0.00075\\\\P(x=13)=(20!)/((20-13)!13!)*0.25^(13)*0.75^(7)=0.00015\\\\P(x=14)=(20!)/((20-14)!14!)*0.25^(14)*0.75^(6)=0.0000257\\\\P(x=15)=(20!)/((20-15)!15!)*0.25^(15)*0.75^(5)=3.426*10^(-6)\\\\`

`P(x=16)=(20!)/((20-16)!16!)*0.25^(16)*0.75^(4)=3.569*10^(-7)\\\\P(x=17)=(20!)/((20-17)!17!)*0.25^(17)*0.75^(3)=2.799*10^(-8)\\\\P(x=18)=(20!)/((20-18)!18!)*0.25^(18)*0.75^(2)=1.555*10^(-9)\\\\P(x=19)=(20!)/((20-19)!19!)*0.25^(19)*0.75^(1)=5.457*10^(-11)\\\\P(x=20)=(20!)/((20-20)!20!)*0.25^(20)*0.75^(0)=9.095*10^(-13)\\\\`

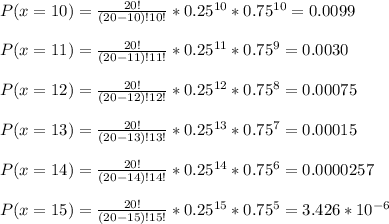
The probability that Pat will pass his exam is:

`P(pass)=0.01386`