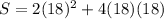Question

A rectangular solid with a square base has a volume of 5832 cubic inches. (Let x represent the length of the sides of the square base and let y represent the height.)

(a) Determine the dimensions that yield the minimum surface area.
(b) Find the minimum surface area.

Answer 1

a) 18 in x 18 in x 18 in

b)
`S = 1944\ in2`

Explanation:

a) Let's call 's' the side of the square base and 'h' the height of the solid.

The surface area is given by the equation:

`S = 2s^2 + 4sh`

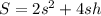
The volume of the solid is given by the equation:

`V = s^2h = 5832`

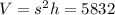
From the volume equation, we have that:

`h = 5832/s^2`

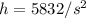
Then, using this value of h in the surface area equation, we have:

`S = 2s^2 + 4s(5832/s^2)`

`S = 2s^2 + 23328/s`

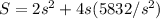
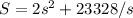
To find the side length that gives the minimum surface area, we can find where the derivative of S in relation to s is zero:

`dS/ds = 4s - 23328/s^2 = 0`

`4s = 23328/s^2`

`4s^3 = 23328`

`s^3 = 23328/4 = 5832`

`s = 18\ inches`

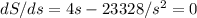
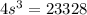
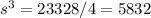
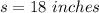
The height of the solid is:

`h = 5832/(18)^2 = 18\ inches`

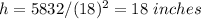
b) The minimum surface area is:

`S = 2(18)^2 + 4(18)(18)`

`S = 1944\ in2`