Question

Find all the complex roots. Leave your answers in polar form with the argument in degrees. The complex fourth roots of -9i.

A. Type an exact answer in the first answer box.
B. Type any angles in degrees between o and 360 needed.)
C. Type all degree measures rounded

Answer 1

Explanation:

Given z = x+iy

The polar form of a complex number
`z = r(cos\theta + isin\theta)`

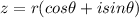
The nth root of the complex number is expressed according to de moivre's theorem as;

`z^{(1)/(n) } = [r(cos\theta + isin\theta)]^{(1)/(n) } \\z^{(1)/(n) } = \sqrt[n]{r} (cos((\theta+2nk)/(n) ) + isin((\theta+2nk)/(n)))`

r is the modulus of the complex number and
`\theta` is the argument

r = √x²+y²

`\theta = tan^(-1) (y)/(x)`

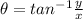
Given z = -9i

r = √0+(-9)²

r = √81

r = 9

`\theta = tan^(-1)(-9)/(0) \\\theta = tan^(-1)-\infty\\\theta = -90^(0)`

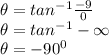
The argument will be equivalent to 180-90 = 90°

The forth root of -9i will be expressed as shown according to de moivre's theorem;

`z_k^{(1)/(4) } = \sqrt[4]{9} (cos((90+2(4)k)/(4) ) + isin((90+2(4)k)/(4)))\\z_k^{(1)/(4) } = \sqrt[4]{9} (cos((90+8k)/(4) ) + isin((90+8k)/(4)))\\`

The complex roots are at when k = 0, 1, 2 and 3

When k = 0;

`z_0 = \sqrt[4]{9} (cos((90)/(4) ) + isin((90)/(4)))\\z_0 = \sqrt[4]{9} (cos(23) + isin(23))\\\\when\ k =1\\z_1 = \sqrt[4]{9} (cos((90+8)/(4) ) + isin((90+8)/(4)))\\z_1 = \sqrt[4]{9} (cos(25 ) + isin(25))\\\\when\ k =2\\z_2 = \sqrt[4]{9} (cos((90+16)/(4) ) + isin((90+16)/(4)))\\z_2 = \sqrt[4]{9} (cos(27 ) + isin(27))\\\\when\ k =3\\z_3 = \sqrt[4]{9} (cos((90+24)/(4) ) + isin((90+24)/(4)))\\z_3 = \sqrt[4]{9} (cos(29 ) + isin(29))\\`

Note that all the degrees are rounded to the nearest whole number.