Question

Consider a sound wave modeled with the equation s(x, t) = 3.00 nm cos(3.50 m−1x − 1,800 s−1t). What is the maximum displacement (in nm), the wavelength (in m), the frequency (in Hz), and the speed (in m/s) of the sound wave?

Answer 1

- maximum displacement = 3.00nm

- λ = 1.79m

- f = 286.47 s^-1

Step-by-step explanation:

You have the following equation for a sound wave:

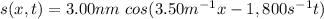`s(x,t)=3.00nm\ cos(3.50m^(-1)x- 1,800s^(-1) t)` (1)

The general form of the equation of a sound wave can be expressed as the following formula:

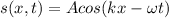`s(x,t)=Acos(kx-\omega t)` (2)

A: amplitude of the wave = 3.00nm

k: wave number = 3.50m^-1

w: angular frequency = 1,800s^-1

- The maximum displacement of the wave is given by the amplitude of the wave, then you have:

maximum displacement = A = 3.00nm

- The wavelength is given by :

`\lambda=(2\pi)/(k)=(2\pi)/(3.50m^(-1))=1.79m`

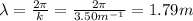
The values for the wavelength is 1.79m

- The frequency is:

`f=(\omega)/(2\pi)=(1,800s^(-1))/(2\pi)=286.47s^(-1)`

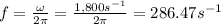
The frequency is 286.47s-1