Question

You were hired as a geotechnical engineer in the XYZ Construction company. Your boss has asked you to estimate the settlement of a new building project that your firm just won the bid. Based on your extensive knowledge on geotechnical engineering and statistical analysis, you estimate that the settlement of the building will not exceed 2 inches with 95% probability. From a record of performance of many similar structures built on similar soil conditions, you also find that the coefficient of variation of the settlement is 20%. After showing the calculation to your boss, she still has few concerns about the settlement.

Requried:
Assuming a normal distribution is used to model the settlement of this project, your boss asks you to give her the probability that this building will settle more than 2.5 inches

Answer 1

Probability = 0.10565

Explanation:

Given:

Mean, u = 2

x = 2.5

CV = 20% = 0.2

To find standard deviation
`\sigma` use the formula:

`CV = (\sigma)/(u)`

`0.2 = (\sigma)/(2)`

`\sigma = 0.2 * 2`

`\sigma = 0.4`

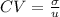
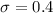
Find Z, using the formula:

`Z = (x - u)/(\sigma)`

`Z = (2.5 - 2)/(0.4)`

`Z = (0.5)/(0.4)`

`Z = 1.25`

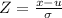
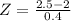
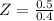
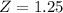
Using the p value table,

P(x > 1.25) = 0.10565

Therefore, The probability that this building will settle more than 2.5 inches is 0.10565