Answer:
The surface area of the cube decreasing at a rate of 3.33 square inches/min.
Explanation:
It is given that, the volume of a cube is decreasing at a rate of 0.5 cubic inches/min.
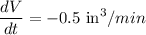 ...(1)
...(1)
We know that, volume of a cube is
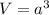
Differentiate w.r.t. t.
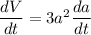

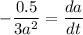 ...(2)
...(2)
Surface area of the cube is
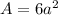
Differentiate w.r.t. t.
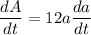

![[Using (2)]](https://img.qammunity.org/2021/formulas/mathematics/college/wy2nlppnsk7ncrfebpacu7flzcnruu0urr.png)

We need to find how fast is the surface area of the cube decreasing when the length of an edge is 0.6 inches.
Substitute a=0.6 in the above equation.
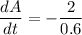
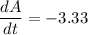
Therefore, the surface area of the cube decreasing at a rate of 3.33 square inches/min.