Question

Consider writing onto a computer disk and then sending it through a certifier that counts the number of missing pulses. Suppose this number x has a Poisson distribution with parameter μ = 0.5. (Round your answers to three decimal places.)

(a) What is the probability that a disk has exactly one missing pulse?
(b) What is the probability that a disk has at least two missing pulses?
(c) lf two disks are independently selected, what is the probability that neither contains a missing pulse?

Answer 1

Explained below.

Explanation:

The random variable X is defined as the number of missing pulses and follows a Poisson distribution with parameter (μ = 0.50).

The probability mass function of X is as follows:

`P(X=x)=(e^(-\mu)\ \mu^(x))/(x!);\ x=0,1,2,3...`

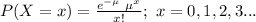
(a)

Compute the probability that a disk has exactly one missing pulse as follows:

`P(X=1)=(e^(-0.50)\ 0.50^(1))/(1!)=0.3033`

Thus, the probability that a disk has exactly one missing pulse is 0.3033.

(b)

Compute the probability that a disk has at least two missing pulses as follows:

`P(X\geq 2)=1-P(X<2)\\`

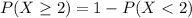
`=1-[P(X=0)+P(X=1)]\\=1-[(e^(-0.50)\ 0.50^(0))/(0!)+(e^(-0.50)\ 0.50^(1))/(1!)]\\=1-0.6065-0.3033\\=0.0902`

Thus, the probability that a disk has at least two missing pulses is 0.0902.

(c)

It is provided that the two disks selected are independent of each other.

The probability that a disk has no missing pulses is:

`P(X=0)=(e^(-0.50)\ 0.50^(0))/(0!)=0.6065`

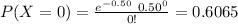
Compute the probability that neither of the two disks contains a missing pulse as follows:

`P(X_(1)=0,\ X_(2)=0)=P(X_(1)=0)* P(X_(2)=0)`

`=0.6065* 0.6065\\=0.367842\\\approx 0.3678`

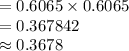
Thus, the probability that neither of the two disks contains a missing pulse is 0.3678.