Question

A point charge of -4.28 pC is fixed on the y-axis, 2.79 mm from the origin. What is the electric field produced by this charge at point P, which is on the x-axis, 9.83 mm from the origin

Answer 1

The electric field at point P produced by a charge of -4.28 pC located 9.83 mm away can be found using the formula E = kQ/r² with appropriate unit conversions.

Step-by-step explanation:

The electric field produced by a point charge can be calculated using Coulomb's law, which is given by the formula E = kQ/r², where E is the electric field, k is Coulomb's constant (8.988 × 10⁹ N·m²/C²), Q is the charge, and r is the distance from the charge to the point of interest. Given a charge of -4.28 pC and a distance of 9.83 mm from the origin along the x-axis, first convert the charge to Coulombs (-4.28 pC = -4.28 × 10⁻±² C) and the distance to meters (9.83 mm = 9.83 × 10⁻³ m). Then, use the formula to calculate the strength of the electric field at point P.

Answer 2

E = (-3.61^i+1.02^j) N/C

magnitude E = 3.75N/C

Step-by-step explanation:

In order to calculate the electric field at the point P, you use the following formula, which takes into account the components of the electric field vector:

`\vec{E}=-k(q)/(r^2)cos\theta\ \hat{i}+k(q)/(r^2)sin\theta\ \hat{j}\\\\\vec{E}=k(q^2)/(r)[-cos\theta\ \hat{i}+sin\theta\ \hat{j}]` (1)

Where the minus sign means that the electric field point to the charge.

k: Coulomb's constant = 8.98*10^9Nm^2/C^2

q = -4.28 pC = -4.28*10^-12C

r: distance to the charge from the point P

The point P is at the point (0,9.83mm)

θ: angle between the electric field vector and the x-axis

The angle is calculated as follow:

`\theta=tan^(-1)((2.79mm)/(9.83mm))=74.15\°`

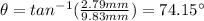
The distance r is:

`r=√((2.79mm)^2+(9.83mm)^2)=10.21mm=10.21*10^(-3)m`

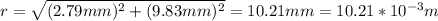
You replace the values of all parameters in the equation (1):

`\vec{E}=(8.98*10^9Nm^2/C^2)(4.28*10^(-12)C)/((10.21*10^(-3)m))[-cos(15.84\°)\hat{i}+sin(15.84\°)\hat{j}]\\\\\vec{E}=(-3.61\hat{i}+1.02\hat{j})(N)/(C)\\\\|\vec{E}|=√((3.61)^2+(1.02)^2)(N)/(C)=3.75(N)/(C)`

The electric field is E = (-3.61^i+1.02^j) N/C with a a magnitude of 3.75N/C