Question

You need 660 mL of a 40% alcohol solution. On hand, you have 35% alcohol mixture. You also have a 95% alcohol mixture. How much of each mixture will you need to add to obtain the desired solution?

You will need...
A. ___ mL of the 35% solution
B. ___ mL of the 95% solution

Answer 1

A. 605 mL of the 35% solution

B. 55 mL of the 95% solution

Explanation:

It is given that, you need 660 mL of a 40% alcohol solution. On hand, you have 35% alcohol mixture. You also have a 95% alcohol mixture.

Let x and y be the amount of 35% alcohol solution and 95% alcohol solution (in mL) respectively.

So,

Amount equation:
`x+y=660` ...(1)

Alcohol equation :
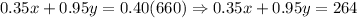`0.35x+0.95y=0.40(660)\Rightarrow 0.35x+0.95y=264` ...(2)

On solving (1) and (2), we get

`0.35(660-y)+0.95y=264`

`231-0.35y+0.95y=264`

`0.6y=264-231`

`y=(33)/(0.6)`

`y=55`

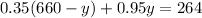
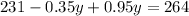
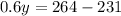
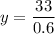
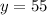
Now, substitute y=55 in (1).

`x+55=660`

`x=660-55`

`x=605`

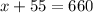
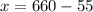
Therefore, we need 605 mL of the 35% solution and 55 mL of the 95% solution.