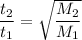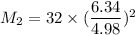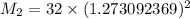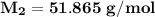Answer:
The molar mass of the unknown gas is
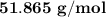
Step-by-step explanation:
Let assume that the gas is O2 gas
O2 gas is to effuse through a porous barrier in time t₁ = 4.98 minutes.
Under the same conditions;
the same number of moles of an unknown gas requires time t₂ = 6.34 minutes to effuse through the same barrier.
From Graham's Law of Diffusion;
Graham's Law of Diffusion states that, at a constant temperature and pressure; the rate of diffusion of a gas is inversely proportional to the square root of its density.
i.e
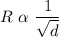
 where K = constant
where K = constant
If we compare the rate o diffusion of two gases;
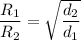
Since the density of a gas d is proportional to its relative molecular mass M. Then;
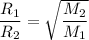
Rate is the reciprocal of time ; i.e

Thus; replacing the value of R into the above previous equation;we have:
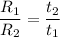
We can equally say: