Question

A random sample of 1007 adults in a certain large country was asked​ "Do you pretty much think televisions are a necessity or a luxury you could do​ without?" Of the 1007 adults​ surveyed, 522 indicated that televisions are a luxury they could do without.

1) Obtain a point estimate for the population proportion of adults in the country who believe that televisions are a luxury they could do without.
2) Verity that the requirements for constructing a confidence interval about p are satisfied.
3) Construct and interpret a 95% confidence inter a for the population proportion of adults in the country who believe a televisions are a luuy ey ou within your choice.
A) We are_____% confident proportion of adults in the country who believe that televisions are a luxury they could do without is between______and_____.
B. There is a______% chance the proportion of adults in the country who believe that televisions are a luxury the could do without is between______and______.
4) Is it possible that a supermaiority (more than 60%) of adults in the country believe that television is a luxury they could do without? Is it likale?

Answer 1

a. p=0.5184

b. All requirements (random, normal, independent) are satisfied.

c. A) We are 95% confident proportion of adults in the country who believe that televisions are a luxury they could do without is between 0.485 and 0.5493.

Explanation:

A point estimate for the population proportion of adults in the country who believe that televisions are a luxury they could do without can be calculated from the sample proportion.

The sample proportion is p=0.5184.

`p=X/n=522/1007=0.5184`

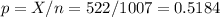
The requirements for constructing a confidence interval about p are:

• Random: the sample is random, so it is satisfied.
• Normal: the values for np and n(1-p) have to be equal or greater than 10. This is satisfied (np=522, n(1-p)=485).
• Independent: as the sample is less than 10% of the population and the sampling is random, this is also satisfied.

We have to calculate a 95% confidence interval for the proportion.

The critical z-value for a 95% confidence interval is z=1.96.

The standard error of the proportion is:

`\sigma_p=\sqrt{(p(1-p))/(n)}=\sqrt{(0.5184*0.4816)/(1007)}\\\\\\ \sigma_p=√(0.000248)=0.0157`

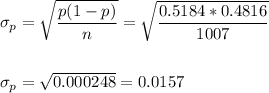
The margin of error (MOE) can be calculated as:

`MOE=z\cdot \sigma_p=1.96 \cdot 0.0157=0.0309`

Then, the lower and upper bounds of the confidence interval are:

`LL=p-z \cdot \sigma_p = 0.5184-0.0309=0.4875\\\\UL=p+z \cdot \sigma_p = 0.5184+0.0309=0.5493`

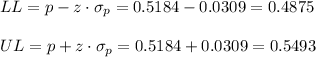
The 95% confidence interval for the population proportion is (0.4875, 0.5493).