Question

You add 50.0 g of ice initially at ‒20.0 °C to 1.00 x 102 mL warm water at 67.0 °C. When all the ice melts, the water temperature is found to be somewhere above 0 °C. Calculate the final temperature of the water.

Answer 1

`T_2=17.8\°C`

Step-by-step explanation:

Hello,

In this case, we can solve this problem by noticing that the heat lost by the warm water is gained by the ice in order to melt it:

`Q_(water)=-Q_(ice)`

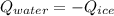
In such a way, the cooling of water corresponds to specific heat and the melting of ice to sensible heat and specific heat also that could be represented as follows:

`m_(water)Cp_(water)(T_2-T_(water))=-m_(ice)\Delta H_(melting,ice)-m_(ice)\Cp_(ice)(T_2-T_(ice))`

Thus, specific heat of water is 4.18 J/g°C, heat of melting is 334 J/g and specific heat of ice is 2.04 J/g°C, thus, we can compute the final temperature as shown below:

`m_(water)Cp_(water)(T_2-T_(water))+m_(ice)Cp_(ice)(T_2-T_(ice))=-m_(ice)\Delta H_(melting,ice)\\\\T_2=(-m_(ice)\Delta H_(melting,ice)+m_(water)Cp_(water)T_(water)+m_(ice)Cp_(ice)T_(ice))/(m_(water)Cp_(water)+m_(ice)Cp_(ice)) \\\\T_2=(-50.0*334+100*4.18*67+50.0*2.04*-20.0)/(100*4.18+50.0*2.04) \\\\T_2=17.8\°C`

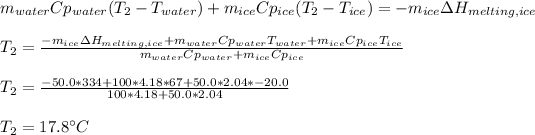
Best regards.