Question

The owner of a fish market has an assistant who has determined that the weights of catfish are normally distributed, with mean of 3.2 pounds and standard deviation of 0.8 pound. If a sample of 4 fish is taken. What is the probability that the sample means will be more than 3.4 pounds?

Answer 1

its 21

Explanation:

its not 21 i really dont know

Answer 2

`P(\bar X>3.4) = 0.385`

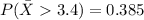
Explanation:

Relevant Data provided according to the question is as follows

`\mu` = 3.2

`\sigma` = 0.8

n = 4

According to the given scenario the calculation of probability that the sample means will be more than 3.4 pounds is shown below:-

`z = (\bar X - \mu)/((a)/(√(n) ) )`

`P(\bar X>3.4) = 1 - P(\bar X\leq 3.4)`

`= 1 - P (\bar X - \sigma)/((a)/(√(n) ) ) \leq \frac{3.4 - \sigma}{\frac{a}√(n) }`

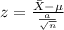
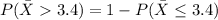
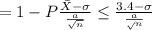
Now, we will solve the formula to reach the probability that is

`= 1 - P (\bar X - 3.2)/((0.8)/(√(4) ) ) \leq \frac{3.4 - 3.2}{\frac{0.8}√(4) }`

`= 1 - P (Z \leq (0.2)/(0.4))`

`= 1 - P (Z \leq 0.5})`

`= 1 - \phi (0.5)`

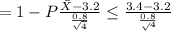
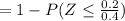
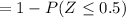
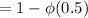
= 1 - 0.6915

= 0.385

Therefore the correct answer is

`P(\bar X>3.4) = 0.385`

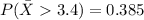
So, for computing the probability we simply applied the above formula.