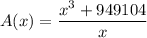Question

A box with a square base and open top must have a volume of 237276 cm^3. We wish to find the dimensions of the box that minimize the amount of material used. Find a formula for the surface area of the box in terms of only x, the length of one side of the square base.[Hint: use the volume formula to express the height of the box in terms of x.]

Answer 1

`A(x)=(x^3+949104)/(x)`

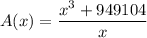
Explanation:

Given a box with a square base and an open top which must have a volume of 237276 cubic centimetre. We want to find a formula for the surface area of the box in terms of only x, the length of one side of the square base.

Let the side length of the base =x

Let the height of the box =h

Since the box has a square base

Volume,

`V=x^2h=237276\\\\h=(237276)/(x^2)`

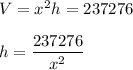
Surface Area of the box = Base Area + Area of 4 sides

`Area, A(x,h)=x^2+4xh`

Substitute h derived above into A(x,h)

`Area=x^2+4x((237276)/(x^2))\\\\A(x)=x^2+(949104)/(x)\\\\A(x)=(x^3+949104)/(x)`

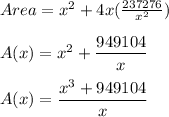
Therefore, a formula for the surface area of the box in terms of only x, the length of one side of the square base is:

`A(x)=(x^3+949104)/(x)`