Answer:
(a) The event that represents success here is the percentage of adults who do not work at all while on summer vacation.
(b) X is a binomial random variable.
(c) The value of p for this binomial experiment is 0.30 or 30%.
(d) P(X = 3) = 0.2541.
(e) The probability that 2 or fewer of the 8 adults do not work during summer vacation is 0.5518.
Explanation:
We are given that in a school it is found that 30% of adults do not work at all while on summer vacation. In a random sample of 8 adults, let X represent the number who do not work during summer vacation.
Let X = the number of adults who do not work during summer vacation
(a) The event that represents success here is the percentage of adults who do not work at all while on summer vacation.
(b) The conditions required for any variable to be considered as a random variable is given by;
- The experiment consists of identical trials.
- Each trial must have only two possibilities: success or failure.
- The trials must be independent of each other.
So, in our question; all these conditions are satisfied which means X is a binomial random variable.
(c) The value of p for this binomial experiment is 0.30 or 30%.
(d) The above situation can be represented through binomial distribution;
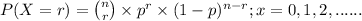
where, n = number of trials (samples) taken = 8 adults
r = number of success = exactly three
p = probability of success which in our question is % of adults who
do not work at all while on summer vacation, i.e; p = 0.25
SO, X ~ Binom(n = 8, p = 0.30)
Now, the probability that exactly 3 adults do not work at all while on summer vacation is given by = P(X = 3)
P(X = 3) =
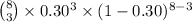
=
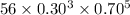
= 0.2541
(e) The probability that 2 or fewer of the 8 adults do not work during summer vacation is given by = P(X
 2)
2)
P(X
 2) = P(X = 0) + P(X = 1) + P(X = 2)
2) = P(X = 0) + P(X = 1) + P(X = 2)
=
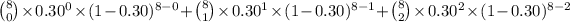
=
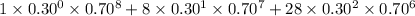
= 0.5518