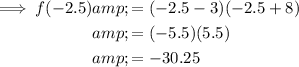Answer:
(a) (3, 0) and (-8, 0)
(b) (-2.5, 0)
(c) x = -2.5
(d) f(-2.5) = -30.25
Explanation:
Given quadratic function:
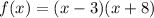
Part (a)
The x-intercepts are when
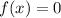
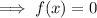
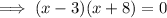
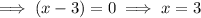
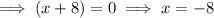
Therefore, the x-intercepts are (3, 0) and (-8, 0)
Part (b)
Midpoint between two points:
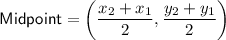
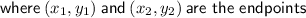
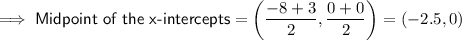
Part (c)
The extreme point of a quadratic function in the form
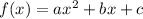 is:
is:
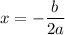
Therefore, expand the function so that it is in standard form:
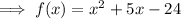
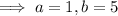
Therefore, the extreme value is:
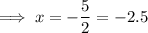
Alternative method
A quadratic function has an extreme value at its vertex.
The x-value of the vertex is the midpoint of the x-intercepts.
Therefore, the extreme value is x = -2.5
Part (d)