Answer:
a)

b)

c) the steady state mass of the drug is 2000 mg
d) t ≅ 153.51 minutes
Explanation:
From the given information;
At time t= 0
an intravenous line is inserted into a vein (into the tank) that carries a drug solution with a concentration of 500
The inflow rate is 0.06 L/min.
Assume the drug is quickly mixed thoroughly in the blood and that the volume of blood remains constant.
The objective of the question is to calculate the following :
a) Write an initial value problem that models the mass of the drug in the blood for t ≥ 0.
From above information given :
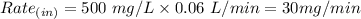
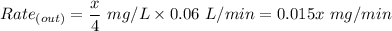
Therefore;
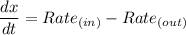
with respect to x(0) = 0

b) Solve the initial value problem and graph both the mass of the drug and the concentration of the drug.
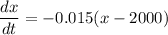

By Using Integration Method:
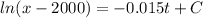
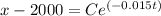
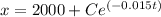
However; if x(0) = 0 ;
Then
C = -2000
Therefore

c) What is the steady-state mass of the drug in the blood?
the steady-state mass of the drug in the blood when t = infinity

x = 2000 - 0
x = 2000
Thus; the steady state mass of the drug is 2000 mg
d) After how many minutes does the drug mass reach 90% of its stead-state level?
After 90% of its steady state level; the mas of the drug is 90% × 2000
= 0.9 × 2000
= 1800
Hence;
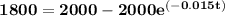

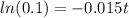
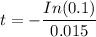
t = 153.5056729
t ≅ 153.51 minutes