Question

A rock is thrown upwards from the roof of an 15.0m high building at 30m/s at an angle of 33 degrees. Find the speed of the rock when it strikes the ground.

Answer 1

The speed of the rock when it strikes the ground is 34.55 m/s

Step-by-step explanation:

Given;

height of the building, h = 15 m

initial velocity of the rock, V₀ = 30 m/s

angle of projection, θ = 33°

The velocity of the rock before it strikes the ground, can be calculated from vertical component of the velocity and horizontal component of the velocity.

Vertical component of the velocity,
`V_y`

`V_y^2 = (V_oSin \theta)^2 + 2gh\\\\V_y^2 = (30Sin \ 33)^2 + 2(9.8)(15)\\\\V_y^2 = 266.93 + 294\\\\V_y = √(560.93) \\\\V_y = 23.684 \ m/s`

Horizontal component of the velocity,
`V_x`

`V_x = V_0 Cos\theta\\\\V_x = 30Cos33\\\\V_x = 25.161 \ m/s`

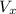
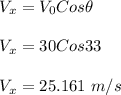
The velocity of the rock when it strikes the ground, V

`V = √(V_y^2 + V_x^2) \\\\V = √(23.684^2 + 25.161^2) \\\\V = 34.55 \ m/s`

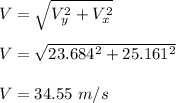
Therefore, the speed of the rock when it strikes the ground is 34.55 m/s