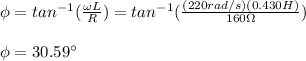Question

You have a 160-Ω resistor and a 0.430-H inductor. Suppose you take the resistor and inductor and make a series circuit with a voltage source that has a voltage amplitude of 30.0 V and an angular frequency of 220 rad/s .

Part A: What is the impedance of the circuit? ( Answer: Z = ? Ω )
Part B: What is the current amplitude? ( Answer: I = ? A )
Part C: What is the voltage amplitude across the resistor? ( Answer: VR = ? V )
Part D: What is the voltage amplitudes across the inductor? ( Answer: VL = ? V )
Part E: What is the phase angle ϕ of the source voltage with respect to the current? ( Answer: ϕ = ? degrees )
Part F: Does the source voltage lag or lead the current? ( Answer: the voltage lags the current OR the voltage leads the current )

Answer 1

A. Z = 185.87Ω

B. I = 0.16A

C. V = 1mV

D. VL = 68.8V

E. Ф = 30.59°

Step-by-step explanation:

A. The impedance of a RL circuit is given by the following formula:

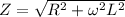`Z=√(R^2+\omega^2L^2)` (1)

R: resistance of the circuit = 160-Ω

w: angular frequency = 220 rad/s

L: inductance of the circuit = 0.430H

You replace in the equation (1):

`Z=√((160\Omega)^2+(220rad/s)^2(0.430H)^2)=185.87\Omega`

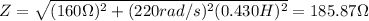
The impedance of the circuit is 185.87Ω

B. The current amplitude is:

`I=(V)/(Z)` (2)

V: voltage amplitude = 30.0V

`I=(30.0V)/(185.87\Omega)=0.16A`

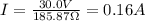
The current amplitude is 0.16A

C. The current I is the same for each component of the circuit. Then, the voltage in the resistor is:

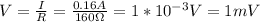`V=(I)/(R)=(0.16A)/(160\Omega)=1*10^(-3)V=1mV` (3)

D. The voltage across the inductor is:

`V_L=L(dI)/(dt)=L(d(Icos(\omega t)))/(dt)=-LIsin(\omega t)\\\\V_L=-(0.430H)(160\Omega)sin(220 t)=68.8sin(220t)\\\\V_L_(max)=68.8V`

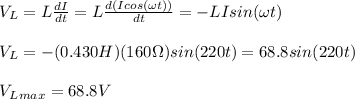
E. The phase difference is given by:

`\phi=tan^(-1)((\omega L)/(R))=tan^(-1)(((220rad/s)(0.430H))/(160\Omega))\\\\\phi=30.59\°`