Question

Joan's Nursery specializes in custom-designed landscaping for residential areas. The estimated labor cost associated with a particular landscaping proposal is based on the number of planting trees, shrubs, and so on to be used for the project. For cost-estimating purposes, managers use two hours of labor time for planting of a medium-sized tree. Actual times from a sample of 10 plantintings during the past month follow (times in hours):

1.7, 1.5, 2.6, 2.2, 2.4, 2.3, 2.6, 3.0, 1.4, 2.3
With a 0.05 level of significance, test to see whether the mean tree-planting time differs from two hours.
A. State the null and alternative hypotheses.
B. Compute the sample mean.
C. Compute the sample standard deviation.
D. What is the p-value?
E. What is your conclusion?

Answer 1

A) Null and alternative hypothesis

`H_0: \mu=2\\\\H_a:\mu\\eq 2`

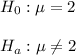
B) M = 2.2 hours

C) s = 0.52 hours

D) P-value = 0.255

E) At a significance level of 0.05, there is not enough evidence to support the claim that the mean tree-planting time significantly differs from two hours.

Explanation:

This is a hypothesis test for the population mean.

The claim is that the mean tree-planting time significantly differs from two hours.

Then, the null and alternative hypothesis are:

`H_0: \mu=2\\\\H_a:\mu\\eq 2`

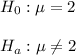
The significance level is 0.05.

The sample has a size n=10.

The sample mean is M=2.2.

As the standard deviation of the population is not known, we estimate it with the sample standard deviation, that has a value of s=0.52.

The estimated standard error of the mean is computed using the formula:

`s_M=(s)/(√(n))=(0.52)/(√(10))=0.1644`

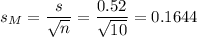
Then, we can calculate the t-statistic as:

`t=(M-\mu)/(s/√(n))=(2.2-2)/(0.1644)=(0.2)/(0.1644)=1.216`

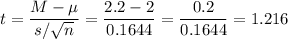
The degrees of freedom for this sample size are:

`df=n-1=10-1=9`

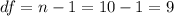
This test is a two-tailed test, with 9 degrees of freedom and t=1.216, so the P-value for this test is calculated as (using a t-table):

`\text{P-value}=2\cdot P(t>1.216)=0.255`

As the P-value (0.255) is bigger than the significance level (0.05), the effect is not significant.

The null hypothesis failed to be rejected.

At a significance level of 0.05, there is not enough evidence to support the claim that the mean tree-planting time significantly differs from two hours.

Sample mean and standard deviation:

`M=(1)/(n)\sum_(i=1)^n\,x_i\\\\\\M=(1)/(10)(1.7+1.5+2.6+. . .+2.3)\\\\\\M=(22)/(10)\\\\\\M=2.2\\\\\\s=\sqrt{(1)/(n-1)\sum_(i=1)^n\,(x_i-M)^2}\\\\\\s=\sqrt{(1)/(9)((1.7-2.2)^2+(1.5-2.2)^2+(2.6-2.2)^2+. . . +(2.3-2.2)^2)}\\\\\\s=\sqrt{(2.4)/(9)}\\\\\\s=√(0.27)=0.52\\\\\\`