Question

A superintendent of a school district conducted a survey to find out the level of job satisfaction among teachers. Out of 53 teachers who replied to the survey, 13 claim they are satisfied with their job.

z equals fraction numerator p with hat on top minus p over denominator square root of begin display style fraction numerator p q over denominator n end fraction end style end root end fraction
The superintendent wishes to construct a significance test for her data. She find that the proportion of satisfied teachers nationally is 18.4%.
What is the z-statistic for this data? Answer choices are rounded to the hundredths place.
a. 2.90
b. 1.15
c. 1.24
d. 0.61

Answer 1

b. 1.15

Explanation:

The z statistics is given by:

`Z = (X - p)/(s)`

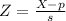
In which X is the found proportion, p is the expected proportion, and s, which is the standard error is
`s = \sqrt{(p(1-p))/(n)}`

Out of 53 teachers who replied to the survey, 13 claim they are satisfied with their job.

This means that
`X = (13)/(53) = 0.2453`

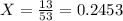
She find that the proportion of satisfied teachers nationally is 18.4%.

This means that
`p = 0.184`

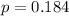
Standard error:

p = 0.184, n = 53.

So

`s = \sqrt{(0.184*0.816)/(53)} = 0.0532`

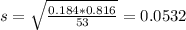
Z-statistic:

`Z = (X - p)/(s)`

`Z = (0.2453 - 0.184)/(0.0532)`

`Z = 1.15`

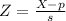
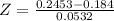
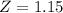
The correct answer is:

b. 1.15