Question

A company produces steel rods. The lengths of the steel rods are normally distributed with a mean of 117.7-cm and a standard deviation of 2.2-cm. For shipment, 29 steel rods are bundled together. Find the probability that the average length of a randomly selected bundle of steel rods is greater than 118.5-cm.

Answer 1

Required probability is 0.9748

Explanation:

given data

mean
`\mu` = 117.7-cm

standard deviation
`\sigma` = 2.2-cm

sample size n = 29

solution

we consider here random variable which represents here length of rod= x

so get here first z that is express as

`Z = (x-\mu)/((\sigma)/(√(n)))`

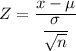
put here value with x value 118.5-cm

`Z = (118.5-117.7)/((2.2)/(√(29)))`

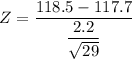
Z = 1.9582

p value is 0.9748

so required probability is 0.9748