Question

The equations 2 x minus y = negative 2, 3 x + 2 y = 5, 4 x minus y = 2, and 22 x + 10 y = 7 are shown on the graph below. On a coordinate plane, there are 4 lines. Green line goes through (0, 2.5) and (1.75, 0). Blue line goes through (0.5, 0) and (1, 2). Pink line goes through (negative 1, 0), and (0, 2). Purple line goes through (negative 0.75, 2.5) and (0, 0.75). Which system of equations has a solution of approximately (–0.3, 1.4)? 2 x minus y = negative 2 and 22 x + 10 y = 7 3 x + 2 y = 5 and 4 x minus y = 2 4 x minus y = 2 and 22 x + 10 y = 7 2 x minus y = negative 2 and 3 x + 2 y = 5

Answer 1

a

Explanation:

did the test

Answer 2

The correct answer is First option:

`22x+10y=7\\ 2x-y=-2`

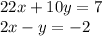
Explanation:

We are given 4 equations:

`22x+10y=7\\ 2x-y=-2\\3x+2y=5\ and\ \\4x-y=2`

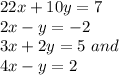
Let us solve the first two:

`22x+10y=7...... (1)\\ 2x-y=-2 ...... (2)`

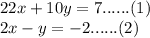
Multiplying (2) with 10 and adding to (1):

`22x+20x=7-20\\\Rightarrow 42x=-12\\\Rightarrow x = -0.2857 \approx -0.3`

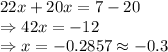
So, approximately, value of x is -0.3.

Putting value of x in (2):

`2 * -0.3 - y =-2\\\Rightarrow y = -0.6+2\\\Rightarrow y = 1.4`

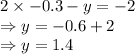
value of x is approximately -0.3 so y is approximately 1.4.

So, the solution is
`\approx` (–0.3, 1.4)

The correct answer is First option:

`22x+10y=7\\ 2x-y=-2`

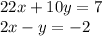
The above two equations have a solution approximately (–0.3, 1.4).