Answer:
The correct option is;
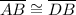 and
and
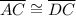
Explanation:
The steps to prove that ΔABC ≅ ΔDBC with the SSS Congruence postulate
We have;
Statement, Reason
BC ≅ BC, Reflexive property
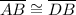 , Option selected
, Option selected
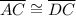 , Option selected
, Option selected
ΔABC ≅ ΔDBC, SSS Congruency Postulate
Therefore, whereby all three sides of the triangles ABC and DBC are congruent, then ΔABC is congruent to ΔDBC.