Question

Suppose that the price​ p, in​ dollars, and the number of​ sales, x, of a certain item follow the equation 6 p plus 3 x plus 2 pxequals69. Suppose also that p and x are both functions of​ time, measured in days. Find the rate at which x is changing when xequals3​, pequals5​, and StartFraction dp Over dt EndFraction equals1.5.

Answer 1

`(dx)/(dt)=-1.3846$ sales per day`

Explanation:

The price​ p, in​ dollars, and the number of​ sales, x, of a certain item follow the equation: 6p+3x+2px=69

Taking the derivative of the equation with respect to time, we obtain:

`6(dp)/(dt) +3(dx)/(dt)+2p(dx)/(dt)+2x(dp)/(dt)=0\\$Rearranging$\\6(dp)/(dt)+2x(dp)/(dt)+3(dx)/(dt)+2p(dx)/(dt)=0\\\\(6+2x)(dp)/(dt)+(3+2p)(dx)/(dt)=0`

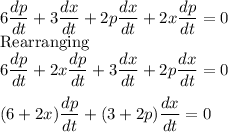
When x=3, p=5 and
`(dp)/(dt)=1.5`

`(6+2(3))(1.5)+(3+2(5))(dx)/(dt)=0\\(6+6)(1.5)+(3+10)(dx)/(dt)=0\\18+13(dx)/(dt)=0\\13(dx)/(dt)=-18\\(dx)/(dt)=-(18)/(13)\\\\(dx)/(dt)=-1.3846$ sales per day`

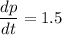
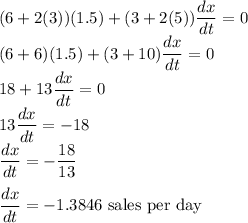
The number of sales, x is decreasing at a rate of 1.3846 sales per day.