Question

The accompanying data represent the total travel tax​ (in dollars) for a​ 3-day business trip in 8 randomly selected cities. A normal probability plot suggests the data could come from a population that is normally distributed. A boxplot indicates there are no outliers.

67.85 78.62 70.28 84.03 79.28 87.72 101.54 97.28
1. Determine a point estimate for the population mean travel tax.
2. Construct and interpret a 95% confidence interval for the mean tax paid for a three-day business trip.
Filling the missing boxes.
The lower bound is $_______and the upper bound is $_______. One can be______% confident that all cities have a travel tax between these values.
The lower bound is $______and the upper bound is $______. The travel tax is between these values for______% of all cities.
The lower bound is $_____and the upper bound is $______. There is a_______% probability that the mean travel tax for all cities is between these values.
The lower bound is $_______and the upper bound is______. One can be______% confident that the mean travel tax for all cities is between these values.
3. What would you recommend to a researcher who wants to increase the precision of the interval, but does not have access to additional data?
A. The researcher could decrease the level of confidence.
B. The researcher could decrease the sample standard deviation.
C. The researcher could increase the level of confidence.
D. The researcher could increase the sample mean.

Answer 1

1. Point estimate M (sample mean): 83.33

2. The lower bound is $73.36 and the upper bound is $93.30. One can be______% confident that the mean travel tax for all cities is between these values.

3. A. The researcher could decrease the level of confidence.

Explanation:

A point esimate for the population mean travel tax can be done with the sample mean.

We can calculate the sample mean as:

`M=(1)/(n)\sum_(i=1)^n\,x_i\\\\\\M=(1)/(8)(67.85+78.62+70.28+84.03+79.28+87.72+101.54+97.28)\\\\\\M=(666.6)/(8)\\\\\\M=83.33\\\\\\`

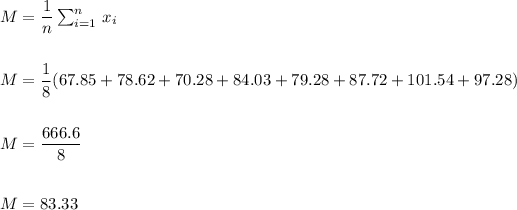
2. We have to calculate a 95% confidence interval for the mean.

The sample mean is M=83.33.

The sample size is N=8.

The population standard deviation is not known, so we have to estimate it from the sample standard deviation and use a t-students distribution to calculate the critical value.

We calculate the sample standard deviation as:

`s=\sqrt{(1)/(n-1)\sum_(i=1)^n\,(x_i-M)^2}\\\\\\s=\sqrt{(1)/(7)((67.85-83.33)^2+(78.62-83.33)^2+(70.28-83.33)^2+. . . +(97.28-83.33)^2)}\\\\\\s=\sqrt{(994.49)/(7)}\\\\\\s=√(142.07)=11.92\\\\\\`

The standard error is:

`s_M=(s)/(√(N))=(11.92)/(√(8))=(11.92)/(2.828)=4.214`

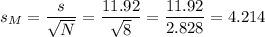
The degrees of freedom for this sample size are:

`df=n-1=8-1=7`

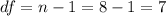
The t-value for a 95% confidence interval and 7 degrees of freedom is t=2.36.

The margin of error (MOE) can be calculated as:

`MOE=t\cdot s_M=2.36 \cdot 4.214=9.97`

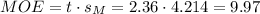
Then, the lower and upper bounds of the confidence interval are:

`LL=M-t \cdot s_M = 83.33-9.97=73.36\\\\UL=M+t \cdot s_M = 83.33+9.97=93.30`

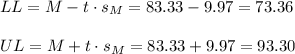
The 95% confidence interval for the mean travel tax is (73.36, 93.30).

We can be 95% confident that the true mean travel tax is within this interval.

3.. If we have no access to additional data, we can not decrease the standard deviation or increase the sample size.

The only way to have a narrower confidence interval is decreasing its level of confidence. With the same sample information, the lower the confidence, the narrower is the interval.