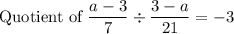Question

What is the quotient? StartFraction a minus 3 Over 7 EndFraction divided by StartFraction 3 minus a Over 21 EndFraction StartFraction negative (a minus 3) squared Over 147 EndFraction StartFraction (a minus 3) squared Over 147 EndFraction 3 –3

Answer 1

b

Explanation:

just correct if wrong

Answer 2

Correct answer is

`\text{Quotient of }(a-3)/(7)/(3-a)/(21) = -3`

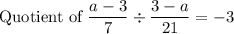
Explanation:

Let us rephrase the given statement mathematically.

We are given the fractions as:

`(a-3)/(7)`

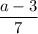
to be divided by:

`(3-a)/(21)`

To find:

`(a-3)/(7)/(3-a)/(21)`

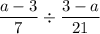
Now, let us have a look at the division rule in fractions:

`(a)/(b) / (c)/(d)`

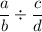
is equivalent to

`(a)/(b) * (d)/(c)`

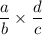
In other words, we say that the second fraction
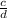`(c)/(d)` is changed to
`(d)/(c)` and
`/` is changed to
`*.`

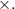
Now solving the given fraction by applying above rules:

`(a-3)/(3)/(3-a)/(21)`

`\Rightarrow (a-3)/(7)* (21)/(3-a)\\\Rightarrow (a-3)/(7)* (21)/(-(a-3))\\\Rightarrow (1)/(1)* (3)/(-1)\\\Rightarrow -3`

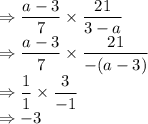
So, correct answer is:

`\text{Quotient of }(a-3)/(7)/(3-a)/(21) = -3`