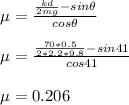Answer:
a) The mass moves a distance of 0.625 m up the slope before coming to rest
b) The distance moved by the mass when it is connected to the spring is 0.6 m
c)
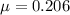
Step-by-step explanation:
Spring constant, k = 70 N/m
Compression, x = 0.50 m
Mass placed at the free end, m = 2.2 kg
angle, θ = 41°
Potential Energy stored in the spring,

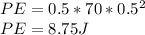
According to the principle of energy conservation
PE = mgh
8.75 = 2.2 * 9.8 * h
h = 0.41
If the mass moves a distance d from the spring
sin 41 = h/d
sin 41 = 0.41/d
d = 0.41/(sin 41)
d = 0.625 m
The mass moves a distance of 0.625 m up the slope before coming to rest
b) If the mass is attached to the spring
According to energy conservation principle:
Initial PE of spring = Final PE of spring + PE of block

The distance moved by the mass when it is connected to the spring is 0.6 m
3) The spring potential is converted to increased PE and work within the system.
mgh = Fd + 0.5kx²...........(1)
d = x , h = dsinθ
kinetic friction force , F = μmgcosθ
mgdsinθ + μmg(cosθ)d = 0.5kd²
mgsinθ + μmgcosθ = 0.5kd
sinθ + μcosθ = kd/(2mg)