Answer:
The angular momentum of the particle about the origin is
![\vec l = -19.305\,k\,\left[kg\cdot (m)/(s) \right]](https://img.qammunity.org/2021/formulas/physics/college/j0t772q2x3zgqg158c0yfrua49wjrt20tb.png) .
.
Step-by-step explanation:
Vectorially speaking, the angular momentum is given by the following cross product:
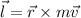
This cross product can be solved with the help of determinants and its properties, that is:

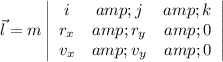
The 3 x 3 determinant is solved by the Sarrus Law:

If
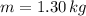 ,
,
![\vec r = 1.50\,i + 2.20\,j\,[m]](https://img.qammunity.org/2021/formulas/physics/college/bjb5xnv0uq5w691d8rfu8qsf89y0qniiil.png) and
and
![\vec v = 4.50\,i-3.30\,j\,\left[(m)/(s) \right]](https://img.qammunity.org/2021/formulas/physics/college/n5awaexrm0r7yxif0isagcz7nmh2z01ep1.png) , the angular momentum of the particle about the origin is:
, the angular momentum of the particle about the origin is:
![\vec l = (1.30\,kg)\cdot \left[\left(1.50\,m\right)\cdot\left(-3.30\,(m)/(s) \right)-\left(2.20\,m\right)\cdot\left(4.50\,(m)/(s) \right)\right]k](https://img.qammunity.org/2021/formulas/physics/college/vbeli0l8thhcbz8dg9nxijh99i4m5n69rx.png)
![\vec l = -19.305\,k\,\left[kg\cdot (m)/(s) \right]](https://img.qammunity.org/2021/formulas/physics/college/j0t772q2x3zgqg158c0yfrua49wjrt20tb.png)
The angular momentum of the particle about the origin is
![\vec l = -19.305\,k\,\left[kg\cdot (m)/(s) \right]](https://img.qammunity.org/2021/formulas/physics/college/j0t772q2x3zgqg158c0yfrua49wjrt20tb.png) .
.