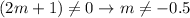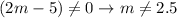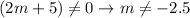1 Answer

Sioux · Answer 1 · 2021-03-27T04:32:53+0000

Answer:

Simplified expression:
( -20m - 26)/((2m+1)(2m-5)(2m+5))

Restrictions:
$m \\eq -0.5, m \\eq 2.5, m \\eq -2.5$

Explanation:

The expression is:

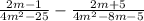
(2m-1)/(4m^2-25) - (2m+5)/(4m^2-8m-5)

We can simplify the denominator of the first fraction:

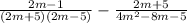
(2m-1)/((2m+5)(2m-5)) - (2m+5)/(4m^2-8m-5)

Then we can simplify the denominator of the second fraction:

(2m-1)/((2m+5)(2m-5)) - (2m+5)/((2m+1)(2m-5))

The least common multiple of the denominators is
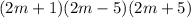(2m+1)(2m-5)(2m+5) , therefore we have:

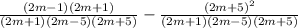
((2m-1)(2m+1))/((2m+1)(2m-5)(2m+5)) - ((2m+5)^2)/((2m+1)(2m-5)(2m+5))

(4m^2-1)/((2m+1)(2m-5)(2m+5)) - (4m^2+20m+25)/((2m+1)(2m-5)(2m+5))

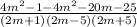
(4m^2-1 - 4m^2 - 20m - 25)/((2m+1)(2m-5)(2m+5))

( -20m - 26)/((2m+1)(2m-5)(2m+5))

The simplified expression is:

( -20m - 26)/((2m+1)(2m-5)(2m+5))

The restrictions are the values of m that makes the denominator zero, so we calculate them using a 'not equal' sign:

$(2m+1) \\eq 0 \rightarrow m \\eq -0.5$

$(2m-5) \\eq 0 \rightarrow m \\eq 2.5$

$(2m+5) \\eq 0 \rightarrow m \\eq -2.5$

Please log in or register to add a comment.