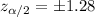Question

Find the critical value z Subscript alpha divided by 2 that corresponds to the given confidence level. 80​%

Answer 1

`Conf= 0.80`

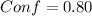
With the confidence level we can find the significance level:

`\alpha =1-0.8=0.2`

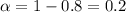
And the value for
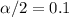`\alpha/2=0.1`. Then we can use the normal standard distribution and we can find a quantile who accumulates 0.1 of the area on each tail and we got:

`z_(\alpha/2)= \pm 1.28`

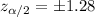
Explanation:

For this problem we have the confidence level given

`Conf= 0.80`

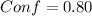
With the confidence level we can find the significance level:

`\alpha =1-0.8=0.2`

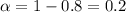
And the value for
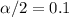`\alpha/2=0.1`. Then we can use the normal standard distribution and we can find a quantile who accumulates 0.1 of the area on each tail and we got:

`z_(\alpha/2)= \pm 1.28`